My earlier post discussed:

• how to measure lead time
• how to analyze lead distribution charts
• how to get better understanding of lead time by breaking down multimodal (work item type mix) lead time data sets into unimodal (by work item type)
• how to establish service-level expectations based on lead time data

As a reminder, the context is creative endeavours in knowledge-work industries.

Now let’s take a closer look at the structure of lead-time distributions and their common elements.

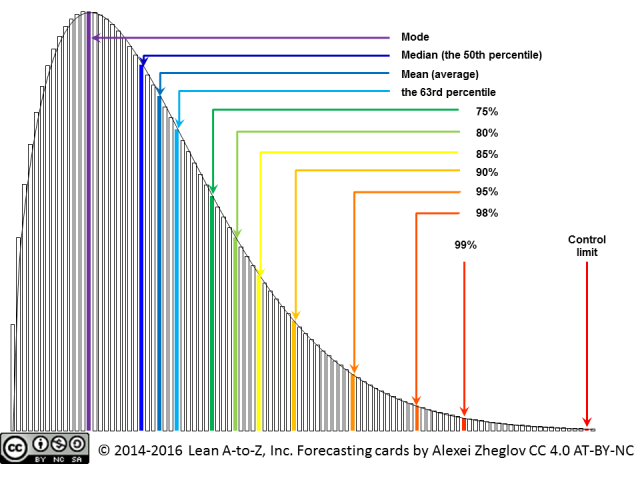
p>Mode. The mode is the most probable or, in other words, the most often occurring number in the data set, or the location of the peak of the distribution curve. In lead time distributions I often observe in delivery processes in knowledge work industries, the mode is often left-shifted and tops the distribution’s asymmetric “hump.” The probability of lead time being less than the mode is small, 18% to 28% observed in distribution shapes common in product development.

The mode is also what people tend to remember well. When asked how long it take to deliver this type of solution, they give the answer their memory is trained on. The trouble is, their memory may be trained on the 18th percentile, so beware of the remaining 82%.

Median. The median is also known as the 50% percentile. If we sorted all numbers in our data set, this one would be right in the middle. Half of the deliveries take more time, half take less. Lead time distributions observed in creative industries are asymmetrical and the median is usually less than the average, sometimes significantly. The ratio of median-to-average of 80% to 90% is quite common in product development. It can drop to 50% in operations and customer care.

Because the median is located on the left side of many other important points on the distribution, it is very useful in establishing short feedback loops to continuously validate forecasting models and project and release plans. If half of the lower-level work items (such as, features in a product release, tasks in a project, and so on) are still being delivered in less than or equal time, in other words, the median is not drifting to the right, the original forecast is still sound.

This insight is due to David J. Anderson, Dan Vacanti and their staff at Corbis. This is a rarely publicized part of their well-known case study from 2006-07. While the project was large and took a long time to deliver in total, there was a feedback loop in it taking only a few days to run and closing almost every day and revalidating the project forecast. The understanding of the median and its role in the distribution enabled this feedback loop.

Average. The average is the easiest to calculate. It connects with the work-in-process (WIP) and throughput in a simple equation known as Little’s Law.

The 63rd percentile. In the Weibull family of distributions, which are often observed, there is one special point, where the over and under probabilities don’t depend on the shape parameter. This point is

Credit to Troy Magennis for pointing this out. Thanks to its unique properties, this percentile can be used in estimating the scale parameter when matching lead time data sets to Weibull distribution.

The 75th percentile. The percentiles between 50th and 75th can be used to estimate the shape parameter if we’re dealing with Weibull distribution and the shape is known to be between 1 and 2, which is common in product development. This owes to another unique property of the 63rd percentile. The math of this estimation is not the purpose of this post, so I’ll save it for future writing.

Higher percentiles (80th and up). The higher percentiles are used in establishing service-level expectations. The average or median are insufficient to define these expectations, because they don’t deal with probabilities of progressively rarer events that the delivery will take longer. The 80th (one in five will take longer), 85th, 90th, 95th, 98th and 99th percentiles are often used for this purpose. These percentiles can be taken from lead time data sets or calculated from Weibull distribution “navigation tables” as multiples of the average (the N-th percentile-to-average ratio depends only on the shape parameter).

The upper control limit. For the purposes of statistical process control and identifying outliers (special-cause variation), we can establish an upper control limit. In creative industries, it is not necessary to establish control limits by calculation. Collaborative inquiry — this project took X days to deliver, do we agree on a single obvious cause that led to the delay? — can be used instead to differentiate between special- and common-cause variation.

If we need to calculate the upper control limit, then adding three standard deviations to the average is plainly incorrect, because the lead time distribution is never Gaussian. With Weibull distribution, we can set the limit at the same probability as being within the average plus three sigma on the Gaussian, which is 99.865%.  Credit to Bruno Chassagne who took this approach assuming the Exponential distribution in IT Operations work and presented the results at Lean Kanban Benelux 2011 conference.  Owing to the properties of Weibull distribution, the control limit is proportional to the lead time average and depends only on the shape parameter. In product development, the ratio of 4 to 6 is common, in operations and customer care, 10 to 12.

Conclusion

Different points on a lead time distribution chart play different roles. Understanding those roles can help us:

1. assess service delivery capabilities
2. set service-level expectations
3. create delivery forecasts
4. create short feedback loops
5. understand workers’ biases
6. manage variation